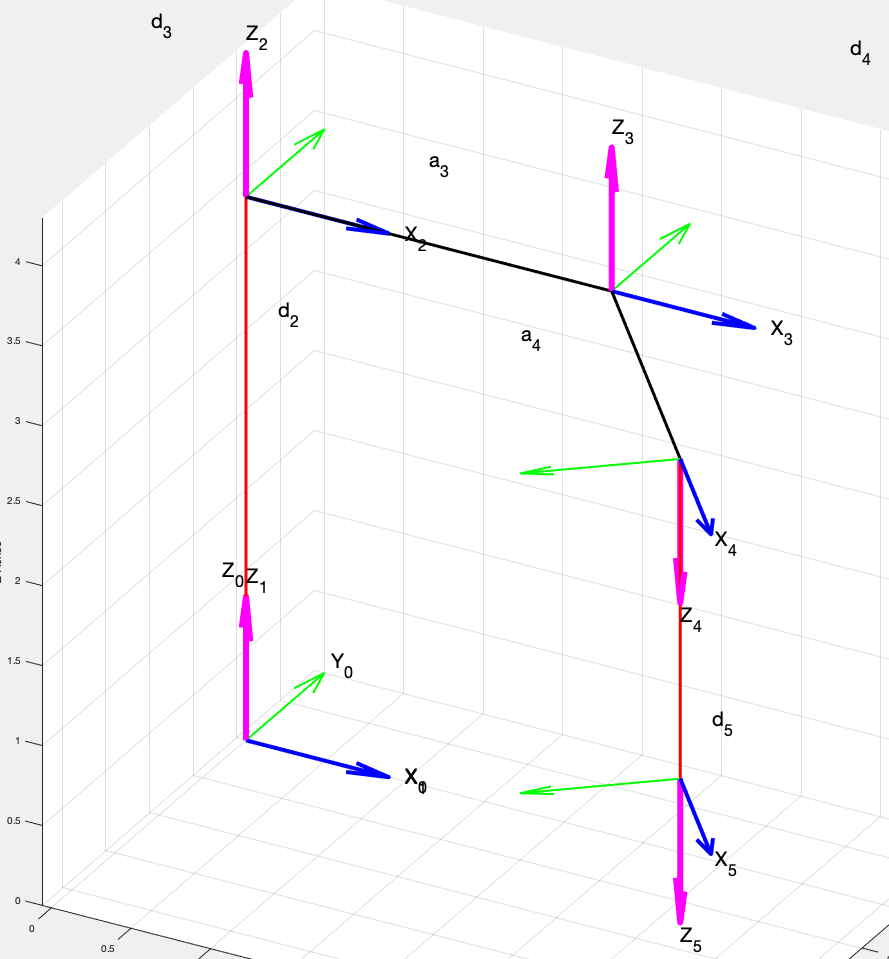
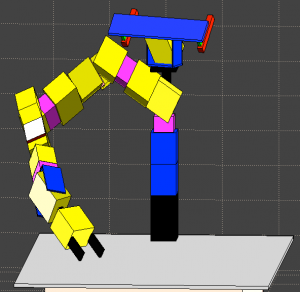
Software
Numerische Lösungsmethoden für ODEs
Vergleich von Euler- und Runge-Kutta-4-Methoden
- Eingabefeld für die DGL:
- Der Benutzer kann eine beliebige DGL der Form
y' = f(t, y)eingeben, z. B.-2 * y,t * y,Math.sin(t) * y, usw. - Die eingegebene DGL wird in eine JavaScript-Funktion umgewandelt.
- Der Benutzer kann eine beliebige DGL der Form
- Dynamische Aktualisierung:
- Wenn der Benutzer die DGL ändert, wird die Funktion
f(t, y)neu erstellt, und die numerischen Lösungen werden neu berechnet.
- Wenn der Benutzer die DGL ändert, wird die Funktion
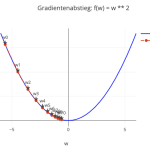
Gradient Descent Visualisierung
Interaktive Visualisierung des Gradientenabstiegsverfahrens
Beispiel:
- Geben Sie
w ** 2als Kostenfunktion ein, um das ursprüngliche Beispiel zu reproduzieren. - Ändern Sie die Kostenfunktion zu
Math.sin(w), um eine andere Funktion zu testen. - Passen Sie die Lernrate, die Anzahl der Iterationen und den Startwert an, um den Gradientenabstieg zu optimieren.
Visualisation-animation of BSTs, B-Trees and Red-Black-Trees. A modified version of David Galles’ visualisation of BSTs, B-Trees and Red-Black-Trees
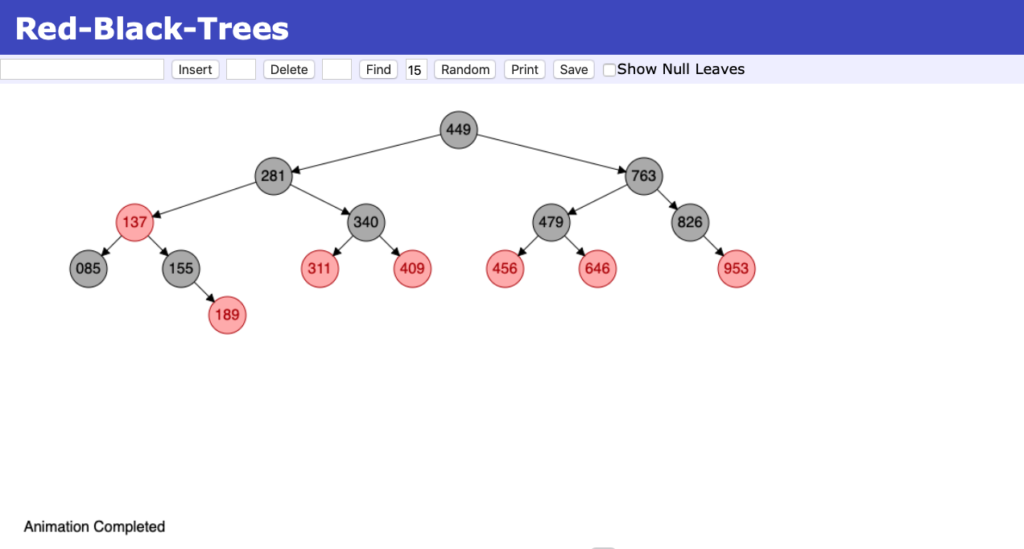
tree-visualisation
A modification of David Galles’ visualisation of BSTs, B-Trees and Red-Black-Trees.
Manual
- Insert: Enter one or more numbers between
0and999. Separate them with your favorite non-digit character sequence. PressInsert. - Delete: Enter a number. Press
Delete. - Find: Enter a number. Press
Find. - Polulate randomly: Enter a count between
1and99. PressRandom. - In-order deth first search: Press
Print. - Export to SVG: Press
Save.
Visualisations
Modifications
Functional
General
- Multiple values can be inserted at once (values can be separated by any non-digit character, causing that…)
- Only numbers can be added
- Maximum value is
999. - A number of random values between
000and999can be inserted - Trees can be exported to SVG.
B-Trees
- Changed degree notation to be in line with Cormen et al. – Introduction to Algorithms
Visual
- Color theme changed
- Canvas font size increased
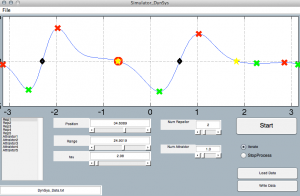 The DynSys-Simulator implement a numerical solution for dynamical systems used in the attractor dynamics approach to robotics. Position, range and number of attractors and repellors can be changed interactively while the phase plot is updated in an closed loop. The simulator visualizes the behavior of the dynamical systems and can give an intuition how it is utilized for the generation of trajectories for mobile robots and redundant manipulators.
The DynSys-Simulator implement a numerical solution for dynamical systems used in the attractor dynamics approach to robotics. Position, range and number of attractors and repellors can be changed interactively while the phase plot is updated in an closed loop. The simulator visualizes the behavior of the dynamical systems and can give an intuition how it is utilized for the generation of trajectories for mobile robots and redundant manipulators.
Download-Link: